Để minh chứng một tam giác sở hữu nhị cạnh cân nhau, tao cần thiết đối chiếu chừng nhiều năm của nhị cạnh cơ và xác lập bọn chúng sở hữu cân nhau hay là không. Dưới đó là nội dung bài viết về: Tam giác cân nặng là gì? Các cách chứng minh tam giác cân?
Tam giác cân nặng là 1 trong loại tam giác sở hữu tối thiểu nhị cạnh cân nhau và nhị góc ở lòng thăng bằng nhau. Cụ thể, nếu như một tam giác sở hữu nhị cạnh cân nhau thì này đó là tam giác cân nặng. Tam giác cân nặng sở hữu lối trung tuyến phân chia tam giác trở thành nhị tam giác thăng bằng nhau và lối cao khởi nguồn từ đỉnh của tam giác vuông góc với lòng cân nặng. Tam giác cân nặng là 1 trong trong mỗi loại tam giác thông thường được dùng vô toán học tập và những nghành nghề khác ví như vẽ hình,
Bạn đang xem: cách chứng minh tam giác cân
Định nghĩa của một tam giác cân nặng vẫn thay cho thay đổi một chút ít trong mỗi năm vừa qua. Ban đầu, Euclid, người thỉnh thoảng được gọi là Euclid của Alexandria và được xem như là Cha đẻ của Hình học tập, vẫn khái niệm một tam giác cân nặng như sau: một tam giác sở hữu nhị cạnh cân nhau. Tuy nhiên, theo gót thời hạn, trong những khi tình thương vẫn như cũ, thuật ngữ vẫn thay cho thay đổi một chút ít. Định nghĩa văn minh rộng lớn của tam giác cân nặng là 1 trong tam giác sở hữu tối thiểu nhị cạnh cân nhau. Sự thay cho thay đổi này còn có vẻ nhỏ, tuy nhiên nó Có nghĩa là, theo gót xài chuẩn chỉnh văn minh, tam giác đều, sở hữu tía cạnh cân nhau, là tình huống quan trọng đặc biệt của tam giác cân nặng.
Trong tình huống tam giác cân nặng sở hữu nhị cạnh cân nhau thì những cạnh cân nhau được gọi là nhị chân của tam giác và cạnh loại tía là lòng.
Nguồn gốc tên: Isosceles lấy thương hiệu kể từ gốc Hy Lạp ‘isos’, tức là cân nhau và ‘skelos’, tức là chân.
2. Tính hóa học của tam giác cân:
Dưới đó là một trong những đặc điểm của tam giác cân:
– Hai cạnh ở lòng của tam giác thăng bằng nhau.
– Hai góc ở lòng của tam giác thăng bằng nhau.
– Đường trung tuyến kẻ kể từ đỉnh cho tới lối cân nặng tiếp tục rời lối cân nặng ở trung điểm của lối cân nặng và bởi 50% chừng nhiều năm lối cân nặng.
– Đường cao kẻ kể từ đỉnh của tam giác vuông góc với lòng cân nặng.
– Tam giác cân nặng sở hữu trọng tâm, trung tuyến, lối cao, tâm lối tròn trặn nội tiếp và tâm lối tròn trặn nước ngoài tiếp đều trùng nhau.
– Diện tích của tam giác cân nặng là nửa đường kính lối tròn trặn nước ngoài tiếp nhân với nửa chu vi tam giác hoặc là tích của độ cao và lòng tam giác phân chia song.
– Tam giác cân nặng là 1 trong trong mỗi tam giác đều, sở hữu tía lối trung trực và một điểm trùng nhau.
– Tam giác bằng phẳng xứng qua chuyện lối cân nặng và qua chuyện lối trung tuyến na ná lối cao.
– Nếu vô một tam giác sở hữu lối trung tuyến bởi lối cao thì tam giác này đó là tam giác cân nặng.
Các đặc điểm bên trên đều là những kỹ năng và kiến thức căn bạn dạng về tam giác cân nặng, tất cả chúng ta hoàn toàn có thể vận dụng vô những việc vô hình học tập và giải quyết và xử lý yếu tố tương quan cho tới tam giác cân nặng.
3. Các loại Tam giác cân:
Nói công cộng, tam giác cân nặng được phân trở thành tía loại không giống nhau:
– Tam giác nhọn cân: Tam giác nhọn cân nặng là tam giác sở hữu cả tía góc nhỏ rộng lớn 90° và tối thiểu nhị vô số những góc của chính nó sở hữu số đo cân nhau. Một ví dụ về những góc của tam giác nhọn cân nặng là 50°, 50° và 80°.
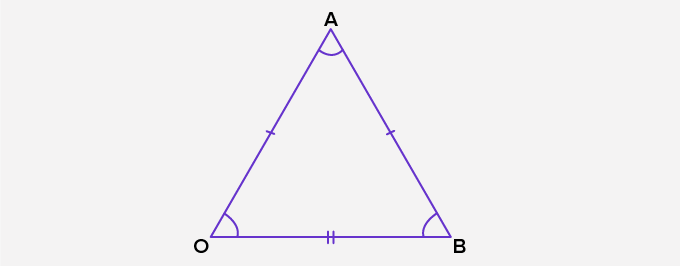
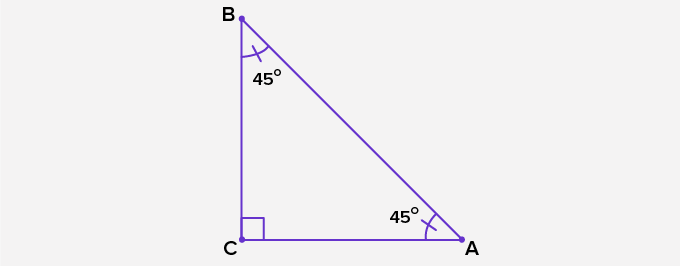
– Tam giác vuông cân: Sau đó là một ví dụ về tam giác vuông sở hữu nhị cạnh (và những góc ứng của chúng) sở hữu số đo cân nhau.
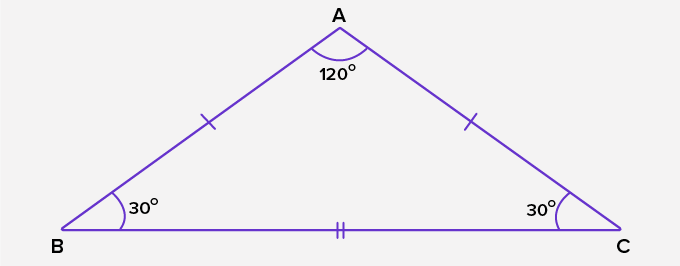
– Tam giác tù cân: Tam giác tù cân nặng là tam giác sở hữu 1 trong những tía góc tù (nằm trong vòng kể từ 90° cho tới 180°) và nhị góc nhọn sót lại sở hữu số đo cân nhau. Một ví dụ về góc tam giác tù cân nặng là 30°, 30° và 120°.
4. Diện tích và chu vi tam giác cân:
– Diện tích của một tam giác cân nặng được mang lại bởi công thức sau:
Diện tích (A) = ½ × lòng (b) × độ cao (h)
– Chu vi của tam giác cân nặng được mang lại bởi công thức:
Chu vi (P) = 2a + lòng (b)
Ở trên đây, ‘a’ là chừng nhiều năm của những cạnh cân nhau của tam giác cân nặng và ‘b’ là chừng nhiều năm của cạnh ko cân nhau loại tía.
Các ví dụ vẫn giải quyết
Ví dụ 1
Chiều cao của một tam giác cân nặng với diện tích S 12 centimet vuông và lòng là 6 centimet là bao nhiêu?
Giải pháp:
Diện tích tam giác cân nặng = ½ x lòng x chiều cao
tức là 12 = ½ x 6 x chiều cao
tức là 12 = 3 x chiều cao
tức là độ cao = 4 cm
Ví dụ 2
Chu vi của một tam giác cân nặng là từng nào, nếu như từng cạnh cân nhau là ‘a’ centimet và cạnh ko cân nhau là ‘b’ cm?
Giải pháp:
Chu vi tam giác cân nặng = tổng những cạnh
Chu vi tam giác cân nặng = (a + a + b) centimet, tức là (2a + b) cm
Xem thêm: Trang web Vebo TV - Danh sách BLV chuyên nghiệp hài hước
Ví dụ 3
Tìm chu vi của một tam giác cân nặng biết lòng là 16 centimet và những cạnh cân nhau là 24 centimet.
Giải pháp:
Công thức tính chu vi tam giác cân nặng, Phường = 2a + b
Ở trên đây, a (cạnh) = 24 centimet và b (đế) = 16 cm
Do cơ, chu vi của một tam giác cân nặng, Phường = 2(24) + 16 = 64 centimet.
Vậy chu vi là 64 centimet.
5. Các cách chứng minh tam giác cân:
Để minh chứng một tam giác là tam giác cân nặng, tao hoàn toàn có thể vận dụng nhị cơ hội sau:
Cách 1: Chứng minh tam giác cơ sở hữu nhị cạnh cân nhau.
Để minh chứng một tam giác sở hữu nhị cạnh cân nhau, tao cần thiết
Ví dụ 1: Trong tam giác ABC sở hữu Δ ABD = Δ ACD . Chứng minh tam giác ABC cân nặng.
+ Chứng minh Theo phong cách 1:
Theo bài bác rời khỏi, tao có:
Δ ABD = Δ ACD
=> AB = AC
=> Tam giác ABC cân nặng bên trên A
Cách 2: Chứng minh tam giác cơ sở hữu nhị góc cân nhau.
Để minh chứng một tam giác sở hữu nhị góc cân nhau, tao cần thiết đo sự cân đối của nhị góc cơ và xác lập bọn chúng sở hữu cân nhau hay là không. Để thực hiện được điều này, tao hoàn toàn có thể dùng thước đo góc nhằm đo sự cân đối của nhị góc và đối chiếu bọn chúng. Nếu nhị góc có tính rộng lớn cân nhau thì tam giác này đó là tam giác cân nặng.
+ Chứng minh Theo phong cách 2:
Theo bài bác rời khỏi, tao có:
∆ ABD = ∆ ACD
=> Góc B = C
=> Tam giác ABC cân nặng bên trên A
Ngoài nhị cơ hội bên trên, tao còn hoàn toàn có thể vận dụng những đặc điểm của tam giác cân nặng nhằm minh chứng một tam giác là tam giác cân nặng. Ví dụ, nếu như tao biết tam giác cơ sở hữu lối trung tuyến bởi lối cao thì tam giác này đó là tam giác cân nặng. Nếu tao biết tam giác cơ sở hữu trung điểm của lối cân nặng phía trên lối trung tuyến thì tam giác này cũng là tam giác cân nặng.
Trong toán học tập, minh chứng một tam giác là tam giác cân nặng không những là sự xác lập đặc điểm của một hình học tập mà còn phải là 1 trong việc hùn nâng cao kĩ năng
Bài tập: Cho tam giác PQR với PQ = quảng bá. Chứng minh tam giác PQR là tam giác cân nặng.
Giải: Ta cần thiết minh chứng PQ = quảng bá và ∠Q = ∠R. PQ = quảng bá (điều khiếu nại vẫn cho) ∠P là góc đằm thắm nhị cạnh PQ và quảng bá.
Ta cần thiết minh chứng rằng ∠Q = ∠R. Khi cơ, tao tiếp tục minh chứng được tam giác PQR là tam giác cân nặng.
Ta có: ∠P = ∠Q + ∠R (theo công thức tổng của những góc vô tam giác). Nhưng vì như thế PQ = quảng bá, nên ∠Q = ∠R (theo lăm le lý cạnh – góc – cạnh).
Vậy, tam giác PQR là tam giác cân nặng.
Kết luận: Tam giác PQR là tam giác cân nặng bởi PQ = quảng bá và ∠Q = ∠R.
Bài tập: Cho tam giác ABC sở hữu AB = AC. Đường trung tuyến BM của tam giác ABC rời lối cao CH bên trên điểm N. Chứng minh rằng tam giác BMN là tam giác cân nặng.
Lời giải: Ta biết AB = AC, vậy tam giác ABC là tam giác cân nặng. Do cơ, lối cao CH cũng chính là lối trung trực của đoạn trực tiếp AB và AC. Như vậy, tao sở hữu BN = công nhân. Do cơ, tam giác BMN sở hữu nhị cạnh BM và BN cân nhau, nên này đó là tam giác cân nặng.
Bài tập: Cho tam giác ABC sở hữu lối trung tuyến BM bởi đoạn trực tiếp AC. Chứng minh rằng tam giác ABC là tam giác cân nặng.
Lời giải: Ta sở hữu BM là lối trung tuyến của tam giác ABC, tức là BM phân chia AC trở thành nhị đoạn cân nhau. Do cơ, tao sở hữu AB = BC và BM = MC. Từ cơ suy rời khỏi tam giác ABC là tam giác cân nặng.
Xem thêm: công ty kim oanh và tân hiệp phát
Bài tập: Cho tam giác ABC sở hữu lối trung tuyến BM. Gọi I là trung điểm của AB và K là trung điểm của AC. Chứng minh rằng IK là lối cao của tam giác BMK.
Lời giải: Ta sở hữu BM là lối trung tuyến của tam giác ABC, tức là BM phân chia AC trở thành nhị đoạn cân nhau. Do cơ, tao sở hữu AB = BC và BM = MC. Từ cơ suy rời khỏi tam giác ABC là tam giác cân nặng và lối trung tuyến BM cũng chính là lối cao của tam giác ABC.
Vì I là trung điểm của AB, nên BI = IA. Tương tự động, tao sở hữu KC = CA. Như vậy, tao sở hữu BI = KC. Do cơ, tam giác BIK là tam giác cân nặng. Vì IK vuông góc với BM và IK rời BM bên trên trung điểm của BM, nên IK là lối cao của tam giác BMK.













Bình luận