hàm số đồng biến nghịch biến

Tìm hiểu lý thuyết và 3 dạng toán phổ cập về hàm số đồng biến nghịch biến: Tìm khoảng tầm đồng vươn lên là nghịch ngợm vươn lên là, ĐK thông số m thỏa mãn nhu cầu. Bài viết lách canh ty chuồn trực tiếp vào việc lúc nào thì hàm đồng vươn lên là và lúc nào thì hàm nghịch ngợm biến? Mang cho tới những mẹo thực hiện bài bác tập dượt một cách nhanh nhất phần mềm vô trắc nghiệm.

Khái niệm

Tính đồng vươn lên là (hay thường hay gọi là tính tăng), tính nghịch ngợm vươn lên là (hay thường hay gọi là tính giảm) là những đặc điểm của một hàm số. Nếu hàm số tăng hoặc rời vô một quãng thì gọi công cộng là đơn điệu trong khúc cơ. Trong tình huống tăng nghiêm nhặt (đang tăng – càng ngày càng tăng) hoặc rời nghiêm nhặt (đang rời – càng ngày càng giảm) thì gọi công cộng là đơn điệu nghiêm nhặt. ^{[1]Trần Văn Hạo và người cùng cơ quan, Giải tích 12, Trang 4 – Phần Tính đơn điệu của hàm số}

Bạn đang xem: hàm số đồng biến nghịch biến

Để xác lập hàm số đồng biến nghịch biến khi nào tớ thông thường lần đạo hàm của hàm số cơ. Nếu đạo hàm dương trong vòng nào là thì hàm số đồng vươn lên là trong vòng cơ, tình huống ngược lại hàm số âm trong vòng nào là thì nghịch ngợm vươn lên là trong vòng cơ. ^{[2]Trần Văn Hạo và người cùng cơ quan, Giải tích 12, Trang 5 – Phần Tính đơn điệu và lốt của đạo hàm}

Định nghĩa

Giả sử K là 1 trong khoảng tầm, một quãng hoặc một nữa khoảng tầm và nó = f(x) là 1 trong hàm số xác lập bên trên K.

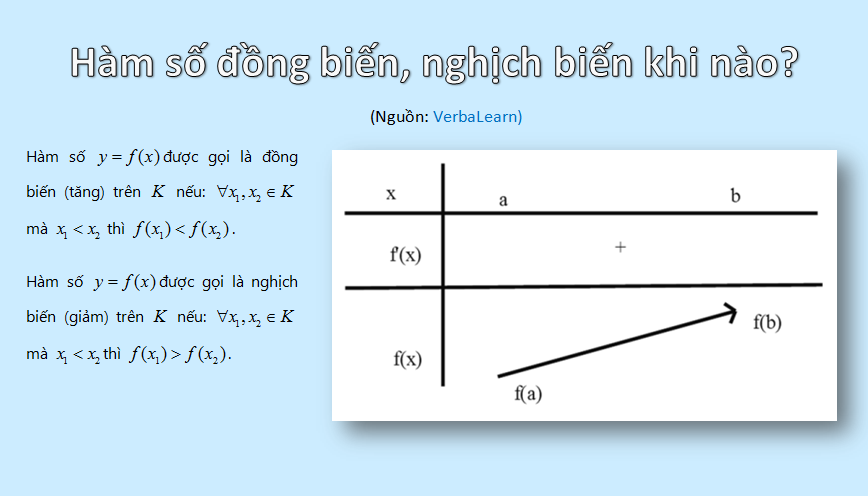
Hàm số nó = f(x) được gọi là đồng vươn lên là (tăng) bên trên K nếu: ∀ x₁, x₂ ∊ K, nếu như x₁ < x₂ thì f(x₁) < f (x₂). ^{[3]Phan Đức Chinh, Toán lớp 9 – Tập 1, Trang 44, 2011 [4]Trần Văn Hạo, Đại số 10 – Tập 1, Trang 36, 2010}

Hàm số nó = f(x) được gọi là nghịch ngợm vươn lên là (giảm) bên trên K nếu: ∀ x₁, x₂ ∊ K, nếu như x₁ < x₂ thì f(x₁) > f (x₂). ^{[3]Phan Đức Chinh, Toán lớp 9 – Tập 1, Trang 44, 2011 [4]Trần Văn Hạo, Đại số 10 – Tập 1, Trang 36, 2010}

Điều kiện

Định lí 1: Điều khiếu nại đầy đủ nhằm hàm số đồng biến nghịch biến

Giả sử hàm số f đem đạo hàm bên trên khoảng tầm K. Khi đó:

• Nếu f’(x) > 0, ∀ x ∊ K thì hàm số f đồng vươn lên là bên trên K. ^{[5]Trần Văn Hạo và người cùng cơ quan, Giải tích 12, Trang 6 – Định lí quá nhận}
• Nếu f’(x) < 0, ∀ x ∊ K thì hàm số f nghịch ngợm vươn lên là bên trên K. ^{[5]Trần Văn Hạo và người cùng cơ quan, Giải tích 12, Trang 6 – Định lí quá nhận}
• Nếu f’(x) = 0, ∀ x ∊ K thì hàm số f ko thay đổi bên trên K.

Chú ý: Khoảng K vô tấp tểnh lí bên trên tớ rất có thể thay vì đoạn hoặc 50% khoảng tầm. Khi cơ nên được thêm fake thuyết “Hàm số liên tiếp bên trên đoạn hoặc nửa khoảng tầm đó”. Chẳng hạn:

Nếu hàm số f liên tiếp bên trên đoạn [a;b] và f’(x) > 0, ∀ x ∊ (a;b) thì hàm số f đồng vươn lên là bên trên đoạn [a;b]. Ta thông thường màn trình diễn qua chuyện bảng vươn lên là thiên như sau:

Định lí 2: Điều khiếu nại cần thiết nhằm hàm số đồng biến nghịch biến

Giả sử hàm số f đem đạo hàm bên trên khoảng tầm K. Khi đó:

• Nếu hàm số đồng vươn lên là bên trên khoảng tầm K thì f’(x) ≥ 0, ∀ x ∊ K
• Nếu hàm số nghịch ngợm vươn lên là bên trên khoảng tầm K thì f’(x) ≤ 0, ∀ x ∊ K

Định lí 3. (Mở rộng lớn của tấp tểnh lí 1)

Giả sử hàm số f đem đạo hàm bên trên khoảng tầm K. Khi đó:

• Nếu f’(x) ≥ 0, ∀ x ∊ K và f’(x) = 0 chỉ bên trên hữu hạn điểm nằm trong K thì hàm số f đồng vươn lên là bên trên K.
• Nếu f’(x) ≤ 0, ∀ x ∊ K và f’(x) = 0 chỉ bên trên hữu hạn điểm nằm trong K thì hàm số f nghịch ngợm vươn lên là bên trên K.

Tính chất

Giả sử K là 1 trong khoảng tầm, một quãng hoặc một nữa khoảng tầm và nó = f(x) là 1 trong hàm số xác lập bên trên K. Hàm số đồng vươn lên là hoặc nghịch ngợm vươn lên là bên trên K gọi công cộng là đơn điệu bên trên K. Từ cơ tớ sẽ có được những đặc điểm như sau:

Tính hóa học 1

Nếu hàm số f(x) và g(x) nằm trong đồng vươn lên là (nghịch biến) bên trên D thì hàm số f(x) + g(x) cũng đồng vươn lên là (nghịch biến) bên trên D. Tính hóa học này rất có thể ko đích thị so với hiệu f(x) – g(x)

Tính hóa học 2

Nếu hàm số f(x) và g(x) là những hàm số dương và nằm trong đồng vươn lên là (nghịch biến) bên trên D thì hàm số f(x)․g(x) cũng đồng vươn lên là (nghịch biến) bên trên D. Tính hóa học này rất có thể ko đúng vào lúc những hàm số f(x) và g(x) ko là những hàm số dương bên trên D.

Tính hóa học 3

Cho hàm số u = u(x) xác lập với x ∊ (a;b) và u(x) ∊ (c;d). Hàm số f [u(x)] cũng xác lập với x ∊ (a;b). Ta đem đánh giá sau:

• Giả sử hàm số u = u(x) đồng vươn lên là với x ∊ (a;b). Khi cơ, hàm số f [u(x)] đồng vươn lên là với x ∊ (a;b) ⇔ f(u) đồng vươn lên là với u(x) ∊ (c;d)
• Giả sử hàm số u = u(x) nghịch ngợm vươn lên là với x ∊ (a;b). Khi cơ, hàm số f [u(x)] nghịch ngợm vươn lên là với x ∊ (a;b) ⇔ f(u) nghịch ngợm vươn lên là với u(x) ∊ (c;d)

Phân dạng bài bác tập

Dạng 1. Tìm khoảng tầm đồng vươn lên là – nghịch ngợm vươn lên là của hàm số

Phương pháp giải

Cho hàm số nó = f(x)

– f’(x) > 0 ở đâu thì hàm số đồng vươn lên là ở đấy.

– f’(x) < 0 ở đâu thì hàm số nghịch ngợm vươn lên là ở đấy.

Các quy tắc

– Tính f’(x), giải phương trình f’(x) = 0 lần nghiệm.

– Lập bảng xét lốt f’(x)

– Dựa vô bảng xét lốt và Kết luận.

Bài tập dượt vận dụng

Câu 1. Cho hàm số f(x) đồng vươn lên là bên trên tập dượt số thực ℝ, mệnh đề nào là sau đó là đúng?

A. Với từng x₁ > x₂ ∊ ℝ ⇒ f (x₁) < f (x₂)

B. Với từng x₁, x₂ ∊ ℝ ⇒ f (x₁) > f (x₂)

C. Với từng x₁, x₂ ∊ ℝ ⇒ f (x₁) < f (x₂)

D. Với từng x₁ < x₂ ∊ ℝ ⇒ f (x₁) < f (x₂)

Hướng dẫn giải

Ta có: f(x) đồng vươn lên là bên trên tập dượt số thực ℝ.

⇒ x₁ < x₂ ∊ ℝ ⇒ f (x₁) < f (x₂)

⟹ Chọn D

Câu 2. Cho hàm số f(x) = -2x³ + 3x² – 3x và 0 ≤ a < b. Khẳng tấp tểnh nào là tại đây sai?

A. Hàm số nghịch ngợm vươn lên là bên trên ℝ

B. f (a) > f (b)

C. f (b) < 0

D. f (a) < f (b)

Hướng dẫn giải

Ta có: f’(x) = -6x² + 6x – 3 < 0, ∀ x ∊ ℝ

⇒ Hàm số nghịch ngợm vươn lên là bên trên ℝ.

0 ≤ a < b ⇒ f (0) ≥ f (a) > f (b)

⟹ Chọn D

Dạng 2. Tìm ĐK của thông số m

Phương pháp giải

– Để hàm số đồng vươn lên là bên trên khoảng tầm (a;b) thì f’(x) ≥ 0, ∀ x ∊ (a;b).

– Để hàm số nghịch ngợm vươn lên là bên trên khoảng tầm (a;b) thì f’(x) ≤ 0, ∀ x ∊ (a;b).

*) Riêng hàm số:

. Có TXĐ là tập dượt D. Điều khiếu nại như sau:

– Để hàm số đồng vươn lên là bên trên TXĐ thì y’ > 0, ∀ x ∊ D.

– Để hàm số nghịch ngợm vươn lên là bên trên TXĐ thì y’ < 0, ∀ x ∊ D.

– Để hàm số đồng vươn lên là bên trên khoảng tầm (a;b) thì

– Để hàm số nghịch ngợm vươn lên là bên trên khoảng tầm (a;b) thì

*) Tìm m nhằm hàm số bậc 3 nó = ax³ + bx² + cx + d đơn điệu bên trên ℝ

– Tính nó = 3ax² + 2bx + c là tam thức bậc 2 đem biệt thức ∆.

– Để hàm số đồng vươn lên là bên trên ℝ

– Để hàm số nghịch ngợm vươn lên là bên trên ℝ

Chú ý

Cho hàm số nó = ax³ + bx² + cx + d

– Khi a > 0 nhằm hàm số nghịch ngợm vươn lên là bên trên một quãng có tính nhiều năm vì như thế k ⇔ y’ = 0 đem 2 nghiệm phân biệt x₁, x₂ sao mang đến |x₁ – x₂| = k.

– Khi a < 0 nhằm hàm số đồng vươn lên là bên trên một quãng có tính nhiều năm vì như thế k ⇔ y’ = 0 đem 2 nghiệm phân biệt x₁, x₂ sao mang đến |x₁ – x₂| = k.

Bài tập dượt vận dụng

Câu 1. Hàm số nó = x³ – 3x² + (m – 2) x + 1 luôn luôn đồng vươn lên là khi:

A. m ≥ 5

B. m ≤ 5

C.

D.

Hướng dẫn giải

Ta có: y’ = 3x² – 6x + m – 2

Xem thêm: cách ướp mận ngon

Hàm số đồng vươn lên là bên trên ℝ khi và chỉ khi y’ = 3x² – 6x + m – 2 ≥ 0, ∀ x ∊ ℝ

⇔ ∆’ ≤ 0 ⇔ 15 – 3m ≤ 0 ⇔ m ≥ 5

⟹ Chọn A

Câu 2. Hàm số nó = ⅓x³ – mx² – (3m + 2) x + 1 đồng vươn lên là bên trên ℝ khi m bằng

A.

B.

C. -2 ≤ m ≤ -1

D. -2 < m < -1

Hướng dẫn giải

Ta có: y’ = x² – 2mx – 3m + 2

Hàm số đồng vươn lên là bên trên ℝ khi và chỉ khi y’ = x² – 2mx – 3m + 2 ≥ 0, ∀ x ∊ ℝ

⇔ ∆’ ≤ 0 ⇔ m² + 3m + 2 ≤ 0 ⇔ -2 ≤ m ≤ -1

⟹ Chọn C

Dạng 3. Xét tính đơn điệu hàm số trùng phương

Phương pháp giải

Bước 1: Tìm tập dượt xác định

Bước 2: Tính đạo hàm f’(x) = 0. Tìm những điểm x_i (i= 1, 2,… n) tuy nhiên bên trên cơ đạo hàm vì như thế 0 hoặc ko xác lập.

Bước 3: Sắp xếp những điểm x_i theo gót trật tự tăng dần dần và lập bảng vươn lên là thiên.

Bước 4: Nêu Kết luận về những khoảng tầm đồng vươn lên là, nghịch ngợm vươn lên là của hàm số.

Bài tập dượt vận dụng

Câu 1. Xét tính đơn điệu của từng hàm số sau: nó = x⁴ – 2x² + 1

Hàm số xác lập với từng x ∊ ℝ

y’ = 4x³ – 4x = 4x (x² – 1)

Cho y’ = 0 ⇒ x = 0 hoặc x = -1 hoặc x = 1

Bảng vươn lên là thiên

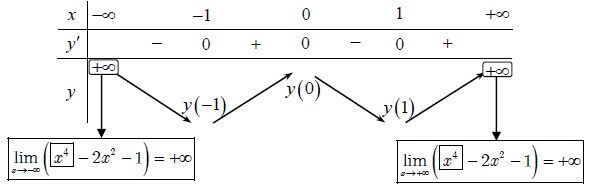
Dựa vô bảng vươn lên là thiên suy ra:

• Hàm số đồng vươn lên là bên trên những khoảng tầm (-1;0) và (1; +∞).
• Hàm số nghịch ngợm vươn lên là bên trên những khoảng tầm (-∞; -1) và (0;1)

Câu 2. Xét tính đơn điệu của từng hàm số sau: nó = -x⁴ + x² – 2

Hàm số xác lập với từng x ∊ ℝ

y’ = -4x³ + 2x = 2x (-2x² + 1)

Cho y’ = 0 ⇒ x = 0 hoặc

hoặc

Bảng vươn lên là thiên

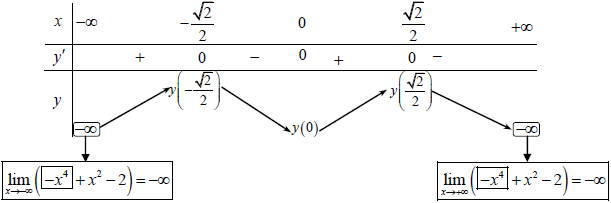
Dựa vô bảng vươn lên là thiên suy ra:

Hàm số đồng vươn lên là bên trên những khoảng tầm

và

Hàm số nghịch ngợm vươn lên là bên trên những khoảng tầm

và

Câu 3. Xét tính đơn điệu của từng hàm số sau: nó = ¼x⁴ + 2x² – 1

Hàm số xác lập với từng x ∊ ℝ

y’ = x³ + 4x = x (x² + 4)

Cho y’ = 0 ⇒ x = 0 (do x² + 4 = 0 vô nghiệm)

Bảng vươn lên là thiên

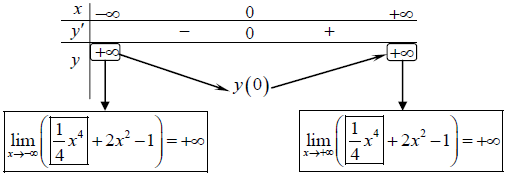
Dựa vô bảng vươn lên là thiên suy ra:

• Hàm số đồng vươn lên là bên trên khoảng tầm (0; +∞)
• Hàm số nghịch ngợm vươn lên là bên trên khoảng tầm (-∞; 0)

Tài liệu tham lam khảo

Chuyên đề tính đơn điệu của hàm số – Thầy Hoàng Xuân Nhàn – 52 trang

Các dạng toán về hàm số đồng vươn lên là, hàm số nghịch ngợm vươn lên là – Thầy Nguyễn hướng dẫn Vương – 59 trang

Khảo sát hàm số và những Việc tương quan – Thầy Phùng Hoàng Em – 17 trang

Bài tập dượt trắc nghiệm VDC tính đơn điệu của hàm số – 34 trang

Bài tập dượt trắc nghiệm tính đơn điệu của hàm số chứa chấp thông số m – VerbaLearn – 28 trang

Bài toán áp dụng cao về tính chất đơn điệu của hàm số – Thầy Nguyễn Công Định – 126 trang